dérivée

dérivée

dérivée [ derive ] n. f.
• 1839; de 1. dériver
♦ Math. Dérivée en un point d'une fonction d'une variable (ou nombre dérivé) :limite vers laquelle tend le rapport de l'accroissement de cette fonction à l'accroissement de la variable lorsque celui-ci tend vers zéro. Dérivées successives, partielles, logarithmiques, géométriques. La dérivée d'une fonction en un point est égale à la pente de la tangente au point correspondant de la courbe qui représente cette fonction. Dérivée à droite (à gauche) d'une fonction. Dérivée (ou fonction dérivée) d'une fonction : fonction qui associe aux valeurs de la variable les nombres dérivés correspondants.

● dérivée nom féminin Fonction dérivée d'une fonction. ● dérivée (expressions) nom féminin Dérivée à droite (respectivement à gauche) d'une fonction f en x0, limite à droite (respectivement à gauche), quand elle existe, en x0, de l'expression , f étant définie sur [x0, a[ (respectivement ]a, x0]). Dérivée d'une fonction f au point x0, limite, quand elle existe, de l'expression 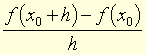quand h tend vers 0. [On la note f′(x0).] Dérivée logarithmique d'une fonction f en x0, réel 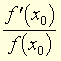[f(x0) ≠ 0]. Dérivée partielle d'une fonction de plusieurs variables, chacune des dérivées des fonctions à une variable obtenues en considérant les autres variables de la fonction comme constantes. (La dérivée de f(x, y, z) par rapport à x se note 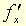, ou 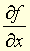. Les dérivées partielles de 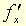, si elles existent, sont appelées dérivées partielles d'ordre 2 et se notent 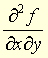, etc., ou 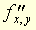. On a : 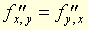.) [Voir tableau ci-contre.]

dérivée
n. f. MATH Limite du rapport entre l'accroissement d'une fonction continue (résultant de l'accroissement de la variable) et l'accroissement de la variable, lorsque ce dernier tend vers zéro.

⇒DÉRIVÉE, subst. fém.
MATH. ,,Limite vers laquelle tend le rapport de l'accroissement de cette fonction à l'accroissement de la variable lorsque ce dernier tend vers zéro`` (DAVAU-COHEN 1972). On peut en général calculer les dérivées secondes et les dérivées successives de tout ordre (Hist. gén. sc., t. 3, vol. 2, 1964, p. 62).
Prononc. et Orth. :[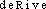]. Ds Ac. 1932. Homon. dérivé, dériver. Étymol. et Hist. 1870 (Lar. 19e). Part. passé fém. substantivé de dériver.

dérivée [deʀive] n. f.
ÉTYM. 1870; de fonction dérivée. → 1. Dériver.
❖
♦ Math. || Dérivée d'une fonction d'une variable : limite vers laquelle tend le rapport de l'accroissement de cette fonction à l'accroissement de la variable lorsque celui-ci tend vers zéro. ⇒ Pente, tangente (à une courbe), taux (d'accroissement). || Dérivées successives, partielles, logarithmiques, géométriques. || Transformation d'une courbe en sa dérivée. || La dérivée d'une fonction en un point est égale à la pente de la tangente au point correspondant de la courbe représentative de cette fonction.
❖
HOM. Dérivé, 1., 2., 3. et 4. dériver.

Encyclopédie Universelle. 2012.

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

  • Derivee — Dérivée  Ne doit pas être confondu avec différentielle. En analyse, le nombre dérivé d une fonction en un point est, si celui ci existe, le coefficient directeur de la tangente au graphe de cette fonction en ce point. C est à dire le… …   Wikipédia en Français

  • Dérivée — En analyse, le nombre dérivé en un point d une fonction à variable et valeurs réelles est le coefficient directeur de la tangente au graphe de cette fonction en ce point. C est le coefficient directeur de l approximation affine de cette fonction… …   Wikipédia en Français

  • DÉRIVÉE — n. f. T. d’Algèbre et de Calcul infinitésimal Dérivée d’une fonction, Limite vers laquelle tend, dans de certaines conditions, cette fonction …   Dictionnaire de l'Academie Francaise, 8eme edition (1935)

  • dérivée — išvestinė statusas T sritis automatika atitikmenys: angl. derivative vok. Ableitung, f; Vorhalt, m rus. производная, f pranc. dérivée, f …   Automatikos terminų žodynas

  • Dérivée (mathématiques élémentaires) — Dérivée  Ne doit pas être confondu avec différentielle. En analyse, le nombre dérivé d une fonction en un point est, si celui ci existe, le coefficient directeur de la tangente au graphe de cette fonction en ce point. C est à dire le… …   Wikipédia en Français

  • Dérivée première — Dérivée  Ne doit pas être confondu avec différentielle. En analyse, le nombre dérivé d une fonction en un point est, si celui ci existe, le coefficient directeur de la tangente au graphe de cette fonction en ce point. C est à dire le… …   Wikipédia en Français

  • Derivee covariante — Dérivée covariante En géométrie différentielle, la dérivée covariante est un outil destiné à obtenir la dérivée d un champ vectoriel sur une variété. Il n existe pas de différence entre la dérivée covariante et la connexion, à part la manière… …   Wikipédia en Français

  • Dérivée Covariante — En géométrie différentielle, la dérivée covariante est un outil destiné à obtenir la dérivée d un champ vectoriel sur une variété. Il n existe pas de différence entre la dérivée covariante et la connexion, à part la manière dont elles sont… …   Wikipédia en Français

  • Derivee directionnelle — Dérivée directionnelle En analyse, la dérivée directionnelle est un outil d analyse à une variable applicable aux fonctions à plusieurs variables. Il permet de décrire les variations infinitésimales d une fonction dans une direction particulière …   Wikipédia en Français

  • Dérivée Directionnelle — En analyse, la dérivée directionnelle est un outil d analyse à une variable applicable aux fonctions à plusieurs variables. Il permet de décrire les variations infinitésimales d une fonction dans une direction particulière. On peut définir cette… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”